As a proud member of the Hungarian team called “senkihaziak”, I managed to solve the following challenge for 300 points in the grab bag category on the 20th DEF CON Capture The Flag contest. The description consisted of an IP address, a port number, a password, and a hint.
Connecting with netcat to the specified IP address and port using TCP and sending the password followed by a newline triggered the server to send back the actual challenge, utilizing ANSI escape sequences for colors.
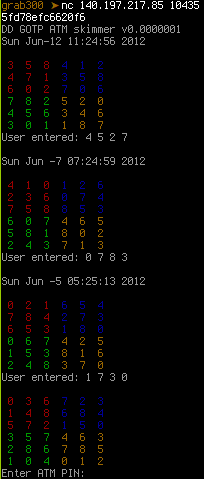
As Buherátor pointed it out, the matrices are parts of a scheme designed to hide PIN codes in random matrices in which only the cardholder knows which digits are part of the PIN code. The service sent three matrices for which the PIN code was known and the challenge was to find the PIN code for the fourth one. As we hoped, the position of the digits within the matrices were the same for all four, so all we needed to do was to find a set of valid positions for each matrix, and apply their intersection to the fourth. I chose Python for the task, and began with connecting to the service.
PW = '5fd78efc6620f6\n'
TARGET = ('140.197.217.85', 10435)
PROMPT = 'Enter ATM PIN:'
def main():
with closing(socket.socket()) as s:
s.connect(TARGET)
s.send(PW)
buf = ''
while PROMPT not in buf:
buf += s.recv(4096)
pin = buffer2pin(buf)
s.send(pin + '\n')
The buffer2pin function parses the response of the service and returns the
digits of the PIN code, separated with spaces. First, the ANSI escape sequences
are stripped from the input buffer. Then, the remaining contents are split into
an array of lines (buf.split('\n')), trailing and leading whitespaces
get stripped (imap(str.strip, ...)), and finally, lines that doesn't contain
a single digit surrounded with spaces get filtered out.
ESCAPE_RE = re.compile('\x1b\\[0;[0-9]+;[0-9]+m')
INTERESTING_RE = re.compile(' [0-9] ')
def buffer2pin(buf):
buf = ESCAPE_RE.sub('', buf)
buf = filter(INTERESTING_RE.search, imap(str.strip, buf.split('\n')))
...
By now, buf contains strings like '3 5 8 4 1 2' and
'User entered: 4 5 2 7', so it's time to build the sets of valid positions.
The initial sets contain all valid numbers, and later, these sets get updated
with an intersection operation. For each example (a matrix with a valid PIN
code) the script joins the six lines of the matrix and removes all spaces.
This results in base holding 36 digits as a string. Finally, the innen for
loop iterates over the four digits in the last line of the current example
(User entered: 4 5 2 7) and finds all occurences in the matrix. The resulting
list of positions is intersected with the set of valid positions for the
current digit (sets[n]). I know that using regular expressions for this
purpose is a little bit of an overkill, but it's
the least evil of the available solutions.
EXAMPLES = 3
DIGITS = 4
INIT_RANGE = range(36)
def buffer2pin(buf):
...
sets = [set(INIT_RANGE) for _ in xrange(DIGITS)]
for i in xrange(EXAMPLES):
base = ''.join(buf[i * 7:i * 7 + 6]).replace(' ', '')
for n, i in enumerate(ifilter(str.isdigit, buf[i * 7 + 6])):
sets[n].intersection_update(m.start() for m in re.finditer(i, base))
...
The only thing that remains is to transform the fourth matrix into a 36 chars long string like the other three, and pick the digits of the resulting PIN code using the sets, which – hopefully – only contain one element each by now.
def buffer2pin(buf):
...
quest = ''.join(buf[3 * 7:3 * 7 + 6]).replace(' ', '')
return ' '.join(quest[digit.pop()] for digit in sets)
The resulting script worked almost perfectly, but after the first run, we found out that after sending a correct PIN code, several more challenges were sent, so the whole logic had to be put in an outer loop. The final script can be found on Gist, and it produced the following output, resulting in 300 points.